4 Normalization, Reduction, and Clustering

source("./preamble.R")
reticulate::source_python("./preamble.py")
analysis_dir <- file.path(getwd(), "analysis_results")
input_dir <- file.path(analysis_dir, "input_files")
output_dir <- file.path(analysis_dir, "output_files")
analysis_asset_dir <- "./assets/analysis_results"
qc_dir <- file.path(output_dir, "qc")
if(!dir.exists(qc_dir)){
  dir.create(qc_dir, recursive = TRUE)
}
pp_dir <- file.path(output_dir, "processing")
if(!dir.exists(pp_dir)){
  dir.create(pp_dir, recursive = TRUE)
}
results_list_file = file.path(analysis_dir, "results_list.rds")
if(!file.exists(results_list_file)){
  results_list <- list()
  saveRDS(results_list, results_list_file)
} else {
  results_list <- readRDS(results_list_file)  
}
source("./helpers.R") # contains the plotDots function

Our quality control steps in Chapter 3 identified the analyzable cells, but these their raw counts need further processing to reveal biological patterns. This chapter covers the essential pre-processing steps to make the data interpretable.

First, normalization adjusts counts to account for technical factors like cell area (i.e., larger cells typically have more counts), enabling fair comparisons between cells. Second, dimensionality reduction (using PCA and UMAP) helps reduce the total number of dimensions in the data (almost 19,000) to a manageable representation that captures key biological variation and allows visualization. Finally, clustering leverages this reduced space to group cells with similar expression profiles, which can be a foundation for downstream analyses like cell typing.

By the end of this chapter, we will have transformed the filtered count matrix into a clustered, low-dimensional dataset and classified cells into groups which, taken together, form our foundation for biological interpretation and spatial analysis. I often get asked “What is the best parameter combination for CosMx data?” and I hope by the end of this chapter you’re able to understand how parameter adjustments impact many of these processing steps.

Let’s begin by loading the data.

adata = ad.read_h5ad(os.path.join(r.analysis_dir, "anndata-1-qc-filtered.h5ad"))

4.1 Two pre-processing workflows

There are two different pre-processing workflows that I use. The first one is borrowed from spatially-unaware scRNA-seq. The main advantage of this approach is that it is fast, the normalization matrix can remain sparse, the values are easy to understand (e.g., counts of gene X per 10,000 or some transformation of such), and often times for WTX data provides the basis for good clustering of cells in downstream UMAP. Moreover, Scanpy and Seurat each have built-in methods for these steps which make it relatively low friction. However, there are cases were this standard (“legacy”) workflow provides unexpected results. One reason is that total counts-based normalization might have unstable variance¹ such that high-expressing housekeeping genes might have high variance and disproportionately effect downstream dimensional reduction and clustering.

The second, newer workflow that I have been using is based on normalization using Pearson Residuals (PR). The approach itself is not new and scanpy has a built-in method for it (i.e., scanpy.experimental.pp.normalize_pearson_residuals). Until recently the main disadvantage for using PR is that it doesn’t scale well to large number of cells that are typical in CosMx SMI¹ and it creates a large, dense normalization matrix that can make analysis and read/writing slower. Fortunately, in many cases I do not need to compute and store such a dense matrix. For example, Dan McGuire recently created the R package scPearsonPCA that can estimate the Principle Components (PCs) of the PR normalized data without needing to convert and use very dense matrices (which we will show below). While this workflow involves converting data between python and R, I generally find the clusters that are derived from such data are comparable to the standard workflow or superior and so I recommend this workflow overall.

In this chapter, I’ll run both the standard and recommended workflows on the colon cancer dataset to provide code for both approaches. I will also do a deep-dive on the choice of UMAP parameters. This particular dataset is a case where the results are more-or-less comparable and I’ll pick the PR data to use throughout the rest of the colon analysis.

Let’s begin. Both options begin the same way: computing the highly variable genes (HVGs). I have found that the pearson_residulas method to detect HVGs (not to be confused with PR normalization) provides stable results for a variety of CosMx SMI WTX experiments.

adata.layers["counts"] = adata.X.copy()

sc.experimental.pp.highly_variable_genes(
    adata,
    flavor='pearson_residuals',
    n_top_genes=4000,
    layer='counts'
)

1

the pearson_residuals ‘flavor’ implement in this function is not the same as the pearson residuals normalization method (see below).

2

generally 3000-5000 is a good starting point here.

Alternative Approach

The pre-processing workflow presented here can be considered a good overall starting point towards understanding the structure of the data. As such I have omitted more complex workflows and tasks such as integrating morphology-based and/or protein-based PCs into the analysis. For a more involved workflow, see our upcoming WTX paper.

The tabs below show both of these workflows. In each workflow, I set the umap parameters to be identical (40 PCs, 15 nearest neighbors, spread = 2 and minimum distance = 0.02). While these are fixed here, see the box Choosing UMAP Parameters below to see how these parameters effect the UMAP visual and the Leiden cluster assignments.

Total Counts Workflow

Workflow: Total counts-based normalization > log transformation > PCA

The procedure below adapts a standard scanpy pipeline. We’ll first normalize each cell the median total counts and then log tranform the data. With this approach I find that scaling the log1p data tends to generate more distinct and biologically relevant clusters so I add that step. Thus, we’ll focus our analysis on the most variable genes found in the dataset. After subsetting down to only these 4000 HVGs, we’ll scale each gene, run PCA, and put these HVG-derivied PCs into the full annData object. On this dataset (466820 cells), this whole process took about a minute.

sc.pp.normalize_total(adata)
sc.pp.log1p(adata) # -> adata.X
adata.layers['TC'] = adata.X.copy()

# Subset to HVGs and get PCs
adata_hvg = adata[:, adata.var.highly_variable].copy()
sc.pp.scale(adata_hvg) # -> adata.X
sc.tl.pca(adata_hvg, svd_solver='auto') 
adata.obsm['X_pca_TC'] = adata_hvg.obsm['X_pca']

Run UMAP and Leiden with the top 40 PCs.

sc.pp.neighbors(adata, n_neighbors=15, n_pcs=40, metric = 'cosine',
  use_rep='X_pca_TC', key_added='neighbors_TC')

UMAP = sc.tl.umap(adata, min_dist=0.02, spread=2, neighbors_key='neighbors_TC', copy=True)

adata.obsm['umap_TC'] = UMAP.obsm['X_umap']
adata.uns['umap_TC_params'] = UMAP.uns['umap']

sc.tl.leiden(adata, resolution=0.5, 
  key_added='leiden_tc', flavor='igraph', 
  n_iterations=2, neighbors_key='neighbors_TC')

Pearson Residuals Workflow

Workflow: Py to R > scPearsonPCA

The scPearsonPCA package estimates the PCs of the PR data without computing and storing a dense normalized matrix. Since it is written in R, we’ll add it to this workflow via reticulate after converting a few objects.

total_counts_per_cell = adata.layers['counts'].sum(axis=1)
total_counts_per_cell = np.asarray(total_counts_per_cell).flatten()

total_counts_per_target = adata.layers['counts'].sum(axis=0)
total_counts_per_target = np.asarray(total_counts_per_target).flatten()

target_frequencies = total_counts_per_target / total_counts_per_target.sum()

adata_hvg = adata[:, adata.var.highly_variable].copy()
hvgs_counts = adata_hvg.layers['counts'].copy().astype(np.int64)

Convert relevant data to R.

library(Matrix)
hvgs_counts <- py$hvgs_counts
rownames(hvgs_counts) <- py$adata_hvg$obs_names$to_list()
colnames(hvgs_counts) <- py$adata_hvg$var_names$to_list()

# the approach we use below expects a sparse matrix with genes (rows) by cells (columns)
t_hvgs_counts <- Matrix::t(hvgs_counts)
t_hvgs_counts <- as(t_hvgs_counts, "CsparseMatrix")

Install the scPearsonPCA package (and remotes), if needed.

remotes::install_github("Nanostring-Biostats/CosMx-Analysis-Scratch-Space",
                         subdir = "_code/scPearsonPCA", ref = "Main")

Run Seurat-style PCA using scPearsonPCA.

library(scPearsonPCA)

total_counts_per_cell <- py$total_counts_per_cell

target_frequencies <- py$target_frequencies
names(target_frequencies) <- py$adata$var_names$to_list()

pcaobj <- sparse_quasipoisson_pca_seurat(
              x = t_hvgs_counts,
              totalcounts = total_counts_per_cell,
              grate = target_frequencies[rownames(t_hvgs_counts)],
              scale.max = 10,
              do.scale = TRUE,
              do.center = TRUE,
              ncores = 5
          )
pca <- pcaobj$reduction.data@cell.embeddings

Add these PCs to the annData object in Python. Run UMAP and Leiden with the top 40 PCs.

adata.obsm["X_pca_pr"] = r.pca

sc.pp.neighbors(adata, n_neighbors=15, n_pcs=40, metric = 'cosine',
  use_rep='X_pca_pr', key_added='neighbors_pr')

UMAP = sc.tl.umap(adata, min_dist=0.02, spread=2, neighbors_key='neighbors_pr', copy=True)
adata.obsm['umap_pr'] = UMAP.obsm['X_umap']
adata.uns['umap_pr_params'] = UMAP.uns['umap']

sc.tl.leiden(adata, resolution=0.5, 
  key_added='leiden_pr', flavor='igraph', 
  n_iterations=2, neighbors_key='neighbors_pr')

Save the annData object.

adata.write_h5ad(
  os.path.join(r.analysis_dir, "anndata-2-leiden.h5ad"),
  compression=hdf5plugin.FILTERS["zstd"],
  compression_opts=hdf5plugin.Zstd(clevel=5).filter_options
)

4.2 Visualizations

Now that we have the UMAP embeddings and the Leiden cluster assignments in the annData object, we can plot the results of the two methods and compare. The easiest way to plot the Leiden clusters in UMAP space is with scnapy’s built-in method, sc.pl.umap; however, since we have non-typical obsm keys, we’ll use the more generic sc.pl.embedding method.

import matplotlib.pyplot as plt
sc.settings.figdir = r.pp_dir
save_dir = r.pp_dir

adata.obs['log10_nCount_RNA'] = np.log10(adata.obs['nCount_RNA'] + 1)
adata.obs['qcflag'] = adata.obs['qcflag'].astype('category')

fig, ((ax1, ax2), (ax3, ax4), (ax5, ax6)) = plt.subplots(3, 2, figsize=(15, 10))

sc.pl.embedding(adata,
                basis='umap_TC',
                color='leiden_tc',
                title='Total Counts (leiden_tc)',
                palette=sc.pl.palettes.default_20,
                ax=ax1,
                show=False)

sc.pl.embedding(adata,
                basis='umap_pr',
                color='leiden_pr',
                title='Pearson Residuals (leiden_pr)',
                palette=sc.pl.palettes.default_20,
                ax=ax2,
                show=False)
                
sc.pl.embedding(adata,
                basis='umap_TC',
                color='log10_nCount_RNA',
                title='Total Counts (log10_nCount_RNA)',
                ax=ax3,
                show=False)

sc.pl.embedding(adata,
                basis='umap_pr',
                color='log10_nCount_RNA',
                title='Pearson Residuals (log10_nCount_RNA)',
                ax=ax4,
                show=False)

sc.pl.embedding(adata,
                basis='umap_TC',
                color='qcflag',
                title='Total Counts (FOV QC Flag)',
                palette=sc.pl.palettes.default_20,
                ax=ax5,
                show=False)

sc.pl.embedding(adata,
                basis='umap_pr',
                color='qcflag',
                title='Pearson Residuals (FOV QC Flag)',
                palette=sc.pl.palettes.default_20,
                ax=ax6,
                show=False)

plt.tight_layout()
filename = "umap_umap_compare.png"
save_path = os.path.join(save_dir, filename)
plt.savefig(save_path)          

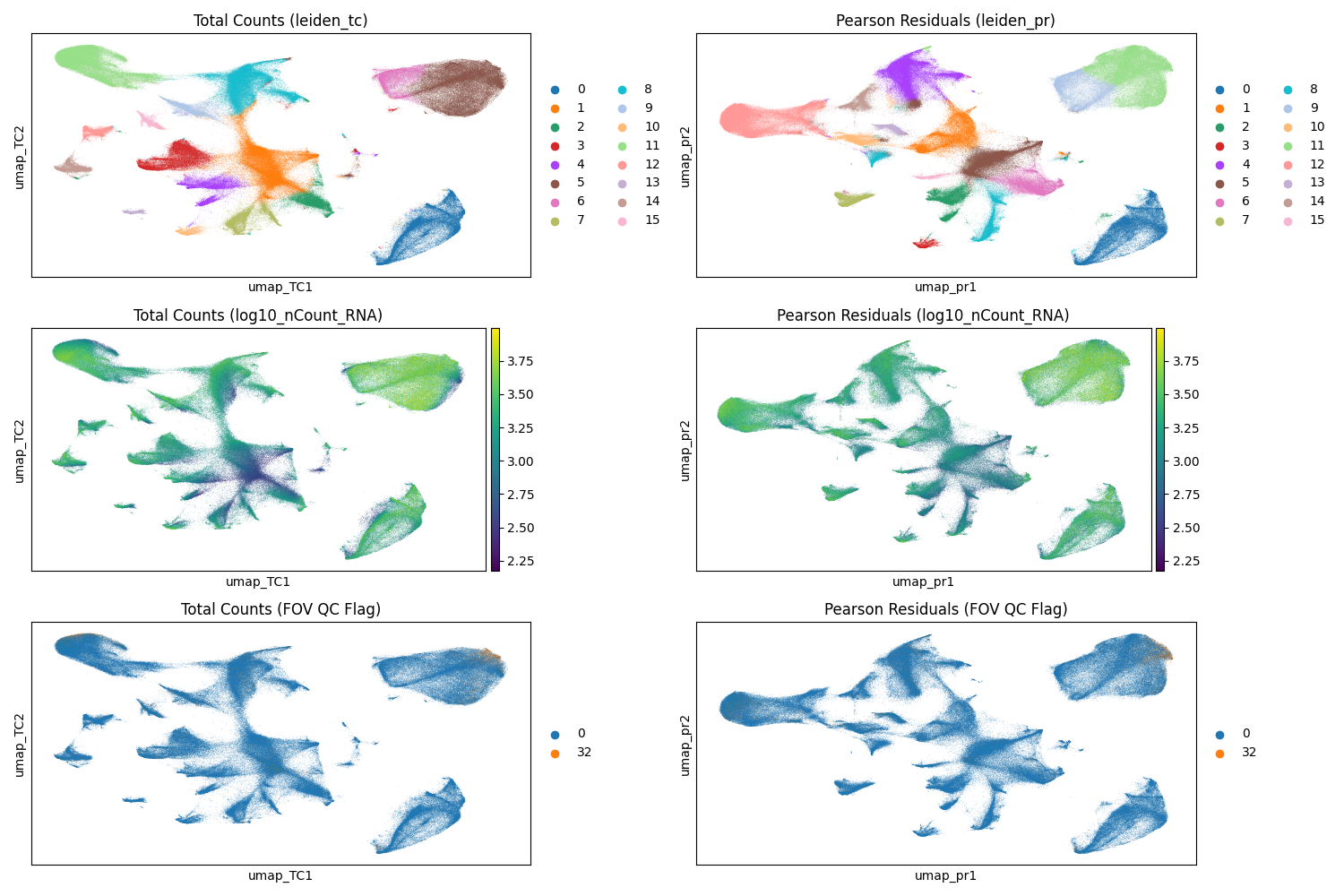
Figure 4.1: UMAP with Leiden clusters from total counts normalization (left) and scPearsonPCA PCs (right). Note that a given cluster label in one plot is not the same as that label in the other plot. Top: Leiden clusters. Middle: cells colored by their total counts. Bottom: cells colored by their QC flag (0 = no flag; 32 = FOV flag; no other flaggeed cells were processed).

Both normalization methods demonstrate effective cluster separation (Figure 4.1). When evaluating these visualizations, it is important to watch for artifacts, particularly sub-clustering driven primarily by total transcript counts, which can signal suboptimal normalization. Additionally, because we retained cells flagged by FOV QC (flag 32), we must verify that these cells do not aggregate into spurious “satellite” clusters which could indicate technical artifacts rather than biological signal. In this dataset, while FOV QC-flagged cells are present in the upper right cluster (Leiden 5 in the total counts workflow and Leiden 11 in the Pearson Residuals workflow), they do not form a distinct artifactual group. Instead, they appear integrated with the dominant cell population, suggesting their distribution is driven by the biology of that region – a hypothesis we will elucidate further in ?sec-celltyping.

We can compare which combination of Leiden clusters a given cell was assigned to:

import pandas as pd
import seaborn as sns

crosstab = pd.crosstab(
    adata.obs['leiden_tc'],
    adata.obs['leiden_pr']
)

crosstab_norm = crosstab.div(crosstab.sum(axis=1), axis=0)

plt.figure(figsize=(12, 10))
sns.heatmap(
    crosstab_norm,
    annot=True,
    fmt=".2f", cmap="viridis",
    linewidths=.5
)

plt.title("Comparison of Leiden clusters derived from TC or PR workflows", fontsize=16)
plt.ylabel("Total Counts (leiden_tc)", fontsize=12)
plt.xlabel("Pearson Residuals (leiden_pr)", fontsize=12)
filename = "leiden_compare_crosstab.png"
save_path = os.path.join(save_dir, filename)
plt.savefig(save_path)     

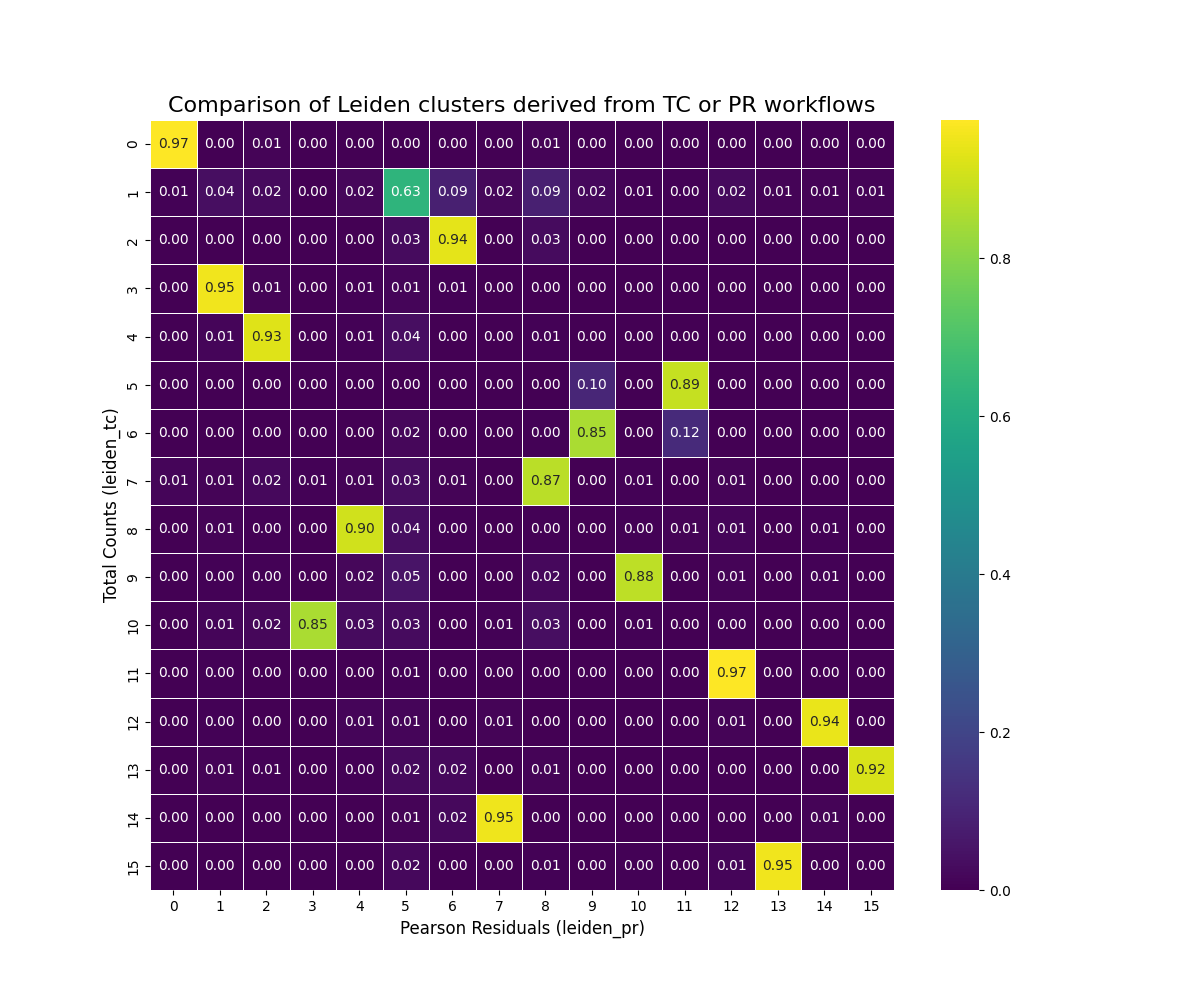
Figure 4.2: Proportion of cells classified with the pure scanpy-based approach compared to the scPearsonPCA-based appraoch.

Figure 4.2 shows a relationship between the clusters derived from our two normalization approaches. Most (15 of 16) Leiden clusters with the total counts approach have more than 85% of cells that are found in a single Leiden cluster for the Pearson Residuals method (e.g., 95% of tc_3 cells mapped to pr_1). One cluster in the total counts approach (tc_1) “split” amongst PR clusters (primarily clusters pr_5, pr_6, and pr_8).

So which is better? With this particular dataset the two approaches are comparable. For the majority of my CosMx SMI WTX analyses I have found the Pearson Residual-based normalization to provide more meaningful biological clusters consistently across datasets so that might be a good overall recommendation – especially if you are working within the R ecosystem. If you are looking for a quick analysis, then the total counts-based approach may work in many cases.

Choosing UMAP Parameters

4.3 Choosing UMAP Parameters

UMAP helps visualize how groups of cells relate to each other in high-dimensional space. While there isn’t one “correct” UMAP layout, some embeddings are more effective than others at revealing underlying biological structure. We have seen in this chapter how having choice in normalization alone (via PCA) can alter the shape of a UMAP plot even when all other parameters are identical (Figure 4.1).

This section explores how commonly adjusted parameters and inputs other than the choice of normalization influence the resulting UMAP visualization, aiming to build intuition for how to tune these parameters effectively in your dataset.

Let’s systematically vary five key factors:

• The quality filtering applied to the input cells. Using only high-quality cells often leads to clearer, tighter clusters representing core biological populations. If filtering was too stringent then entire cell populations might be unrepresented.
• The number of Principal Components (PCs) used. Using a lower number will concetrate on the strongest axes of variation at the cost of reducing any distinction between cell subtypes if that distinction is found in higher PCs. Choosing a higher number of PCs can potentially resolve finer subtypes but also risks incorporating noise, which might slightly blur cluster boundaries or create small, potentially spurious groupings.
• The number of nearest neighbors (n_neighbors). Lower n_neighbors tends to emphasize local cluster separation while higher n_neigbhors tends to form broader clusters.
• The distance metric (metric). Defines the rule for calculating “closeness” between cells. Euclidean measures straight-line distance while cosine measures the angle between gene expression profiles. Since changing this alters which cells are considered “neighbors,” the parameter can have large impacts on the global shape. Euclidean is the default many packages but cosine often provides more biologically meaningful clusters for CosMx SMI data.
• The minimum distance parameter (min_dist). Controls how tightly packed points are within a cluster. Higher values tend to make more diffuse clusters.
• The spread parameter (spread). Controls the separation between clusters. Lower spread tends to bring clusters closer together.

This list isn’t exhaustive, but varying these while keeping others constant will illustrate their core effects. To make this exploration computationally feasible, we will use a representative subsample of 50,000 cells from our quality-flagged dataset. And to make visualization smooth, we’ll only plot at most 500 cells.

Click the radio buttons below to see what effect these parameter have on the UMAP visualization. Some of these changes are gradual while some dramatically alter the shape and configuration of the UMAP embeddings. You’ll note that filtering out the poor quality cells doesn’t merely remove the cells from the UMAP; instead, the inclusion of poorer-quality data can effect the entire UMAP topology. I have also included the Leiden clusters for these cells. The number of PCs and the number of neighbors effect Leiden cluster cell assignment while spread and min_dist do not.

Encouragingly, in this dataset there doesn’t appear to be any UMAP clusters that appear to be made up of cells that were flagged in our FOV QC analysis (Section 3.1). If this was the case, it would suggest that we would want to remove the cells in the effected FOVs.

viewof qc_level = Inputs.radio(["no QC filter", "include FOV QC cells", "filter all flags"], {label: "QC Level", value: "include FOV QC cells"})
viewof n_pcs = Inputs.radio([10, 20, 30, 40, 50], {label: "PCs", value: 30})
viewof n_neighbors = Inputs.radio([15, 30, 50], {label: "Neighbors", value: 30})
viewof metric = Inputs.radio(["euclidean", "cosine"], {label: "Metric", value: "cosine"})
viewof mdist = Inputs.radio([0.01, 0.05, 0.2, 0.5], {label: "Min. distance", value: 0.2})
viewof spread = Inputs.radio([0.5, 1.0, 2.0], {label: "Spread", value: 2.0})
viewof colorby = Inputs.radio(["QC", "Leiden"], {label: "Color by", value: "QC"})

qcMasks = ({
  LOW_COUNTS: 1 << 0, 
  HIGH_COUNTS: 1 << 1, 
  LOW_FEAT: 1 << 2,
  HIGH_FEAT: 1 << 3, 
  LOW_SPLIT: 1 << 4, 
  FOV_QC: 1 << 5, 
  LOW_SBR: 1 << 6
})

flagNames = Object.keys(qcMasks).sort((a, b) => qcMasks[a] - qcMasks[b]);
qcFlagMap = new Map(qc_flags_data.map(d => [d.cell_id, d.qcflag]));

flagColors = {
  const uniqueFlagsInData = Array.from(new Set(qc_flags_data.map(d => d.qcflag))).sort((a, b) => a - b);
  const uniqueFlagsWithZero = Array.from(new Set([0, ...uniqueFlagsInData])).sort((a,b)=> a-b);
  const colors = d3.schemeTableau10;
  const map = {};
  let colorIndex = 0;
  uniqueFlagsWithZero.forEach(flagValue => {
    if (flagValue === 0) { map[flagValue] = "black"; }
    else { map[flagValue] = colors[colorIndex++ % colors.length]; }
  });
  return map;
}

qcColorScale = (flagValue) => flagColors[flagValue ?? 0];

qcFlagLegend = {
  try {
    const uniqueFlagsWithZero = Object.keys(flagColors).map(Number).sort((a,b)=> a-b);
    const tableRows = uniqueFlagsWithZero.map(flagValue => {
      const flagColor = flagColors[flagValue]; // Use static map
      const circles = flagNames.map(name => {
         const mask = qcMasks[name];
         const isSet = (flagValue & mask) > 0;
         const circleFill = isSet ? flagColor : "#e0e0e0";
         const circleSvg = `<svg width="15" height="15"><circle cx="7.5" cy="7.5" r="6" fill="${circleFill}" stroke="${isSet ? 'black' : '#ccc'}" stroke-width="1"></circle></svg>`;
         return `<td style="text-align: center;">${circleSvg}</td>`;
      }).join('');
      const rowHeader = `<th scope="row" style="text-align: right; padding-right: 10px; white-space: nowrap;">
                           <span style="display: inline-block; width: 12px; height: 12px; background-color: ${flagColor}; border: 1px solid #555; margin-right: 5px; vertical-align: middle;"></span>
                           ${flagValue === 0 ? 'Passed' : flagValue}
                         </th>`;
      return `<tr>${rowHeader}${circles}</tr>`;
    }).join('');
    const headerCells = flagNames.map(name =>
      `<th style="height: 100px; text-align: center; vertical-align: bottom; padding-bottom: 5px; font-size: 0.8em; white-space: nowrap;">
         <span style="writing-mode: vertical-lr; transform: rotate(180deg);">${name.replace(/_/g, ' ')}</span>
       </th>`
    ).join('');
    const tableHeader = `<thead><tr><th style="vertical-align: bottom;">Flag Value</th>${headerCells}</tr></thead>`;
    return html`<table style="border-collapse: collapse; margin-top: 10px; font-size: 0.9em; table-layout: fixed;">
                   ${tableHeader}<tbody>${tableRows}</tbody>
                 </table>`;
   } catch (error) {
     console.error("Error generating QC Legend:", error);
     return html`<div>Error generating QC Legend</div>`;
   }
}

leidenScaleAndLegend = {
  let scale, legend;
  try { // Add try...catch
    // Check if query_data is ready and has 'leiden'
    if (!query_data || query_data.length === 0 || !query_data[0].hasOwnProperty('leiden')) {
        console.warn("Leiden data (query_data) not ready for legend/scale.");
        scale = d3.scaleOrdinal().domain(["0"]).range(["grey"]); // Placeholder scale
        legend = html`<div><ul style="list-style: none; padding-left: 0; margin-top: 10px; font-size: 0.9em;">
                        <li style="margin-bottom: 2px;"><span style="display: inline-block; width: 12px; height: 12px; background-color: grey; border: 1px solid #555; margin-right: 5px; vertical-align: middle;"></span> Cluster 0</li>
                      </ul>(Loading...)</div>`; // placeholder
    } else {
        const uniqueClusters = Array.from(new Set(query_data.map(d => d.leiden))).sort((a, b) => a - b);
        scale = d3.scaleOrdinal(d3.schemeTableau10).domain(uniqueClusters);

        const legendItems = uniqueClusters.map(cluster => {
           const color = scale(cluster);
           const clusterLabel = String(cluster);
           return `<li style="margin-bottom: 2px;"><span style="display: inline-block; width: 12px; height: 12px; background-color: ${color}; border: 1px solid #555; margin-right: 5px; vertical-align: middle;"></span> Cluster ${clusterLabel}</li>`;
        }).join('');
        legend = html`<ul style="list-style: none; padding-left: 0; margin-top: 10px; font-size: 0.9em;">${legendItems}</ul>`;
    }
  } catch(error) {
     console.error("Error generating Leiden Legend:", error);
     scale = () => 'grey';
     legend = html`<div>Error generating Leiden Legend</div>`;
  }
  return { scale, legend };
}

leidenColorScale = leidenScaleAndLegend.scale
leidenLegendHtml = leidenScaleAndLegend.legend

d3 = require("d3@7")

width = 500
height = 500
marginTop = 20
marginRight = 20
marginBottom = 30
marginLeft = 40

xScale = d3.scaleLinear().domain([0, 1]).range([marginLeft, width - marginRight])
yScale = d3.scaleLinear().domain([0, 1]).range([height - marginBottom, marginTop])

svg = d3.create("svg")
    .attr("width", width)
    .attr("height", height)
    .attr("viewBox", [0, 0, width, height])
    .attr("style", "max-width: 100%; height: auto;");

xAxis = d3.axisBottom(xScale)
    .ticks(width / 80)
    .tickSizeOuter(0)
    .tickSizeInner(-(height - marginTop - marginBottom));

yAxis = d3.axisLeft(yScale)
    .ticks(height / 40)
    .tickSizeOuter(0)
    .tickSizeInner(-(width - marginLeft - marginRight));

gx = svg.append("g")
    .attr("class", "x-axis")
    .attr("transform", `translate(0,${height - marginBottom})`)
    .call(xAxis);

gy = svg.append("g")
    .attr("class", "y-axis")
    .attr("transform", `translate(${marginLeft},0)`)
    .call(yAxis);

svg.selectAll(".tick line")
   .attr("stroke-opacity", 0.1);

svg.append("text")
    .attr("x", width - marginRight)
    .attr("y", height - marginBottom - 4)
    .attr("fill", "currentColor")
    .attr("text-anchor", "end")
    .text("UMAP 1 →");

svg.append("text")
    .attr("x", marginLeft + 4)
    .attr("y", marginTop)
    .attr("fill", "currentColor")
    .attr("text-anchor", "start")
    .attr("dominant-baseline", "hanging")
    .text("↑ UMAP 2");

-
svg.append("clipPath")
    .attr("id", "clip")
  .append("rect")
    .attr("x", marginLeft)
    .attr("y", marginTop)
    .attr("width", width - marginLeft - marginRight)
    .attr("height", height - marginTop - marginBottom);

pointGroup = svg.append("g")
    .attr("fill", "black")
    .attr("clip-path", "url(#clip)");

{ // Reactive block
  const updateVisualization = () => {
    const duration = 750;
    
    const currentScale = colorby === "QC" ? qcColorScale : leidenColorScale;

    if (!currentScale) { 
        console.error("Scale missing"); 
        return; 
    }
    
    if (!query_data || query_data.length === 0) {
       console.warn("No data available for plotting.");
       pointGroup.selectAll("circle").transition().duration(duration).attr("opacity", 0).remove();
       return; 
    }

    const xExtent = d3.extent(query_data, d => d.umap_1);
    const yExtent = d3.extent(query_data, d => d.umap_2);

    const xPad = (xExtent[1] - xExtent[0]) * 0.05;
    const yPad = (yExtent[1] - yExtent[0]) * 0.05;

    xScale.domain([xExtent[0] - xPad || -1, xExtent[1] + xPad || 1]);
    yScale.domain([yExtent[0] - yPad || -1, yExtent[1] + yPad || 1]);

    svg.select(".x-axis")
      .transition().duration(duration)
      .call(xAxis)
      .on("start", () => {
         svg.selectAll(".x-axis .tick line").attr("stroke-opacity", 0.1);
      });

    svg.select(".y-axis")
      .transition().duration(duration)
      .call(yAxis)
      .on("start", () => {
         svg.selectAll(".y-axis .tick line").attr("stroke-opacity", 0.1);
      });

    pointGroup.selectAll("circle")
      .data(query_data, d => d.cell_id)
      .join(
        enter => enter.append("circle")
            .attr("cx", d => xScale(d.umap_1)) 
            .attr("cy", d => yScale(d.umap_2))
            .attr("r", 2.5)
            .attr("fill", d => {
                try {
                    const valueToColor = colorby === "QC" ? qcFlagMap.get(d.cell_id) : d.leiden;
                    return currentScale(valueToColor) || 'grey';
                } catch(e) { return 'grey'; }
            }) 
            .attr("opacity", 0)
            .call(enter => enter.transition().duration(duration).attr("opacity", 0.8)),
        
        update => update
            .call(update => update.transition().duration(duration)
                .attr("cx", d => xScale(d.umap_1))
                .attr("cy", d => yScale(d.umap_2))
                .attr("fill", d => { 
                    try {
                        const valueToColor = colorby === "QC" ? qcFlagMap.get(d.cell_id) : d.leiden;
                        return currentScale(valueToColor) || 'grey';
                    } catch(e) { return 'grey'; }
                })
                .attr("opacity", 0.8)
             ),
        
        exit => exit
            .call(exit => exit.transition().duration(duration).attr("opacity", 0).remove())
      );
  };
  
  try { 
    updateVisualization();
  } catch(error) {
    console.error("Error during D3 updateVisualization:", error);
  }

  return svg.node(); 
}

In the dot plot on the bottom left provides a QC flag legend. For example, QC flag ‘5’ represents cells that were flagged for having low counts and low features whereas QC flag ‘96’ represents cells that wee flagged for FOV QC as wells as low SBR.

If you want to further explore this subset, you can examine the query_data and qc_flags_data dataframes below.

For the remainder of this chapter, I will focus on the PR-based method.

I find it’s helpful to:

1. Have more control of the plotting aesthetics and label multiple sub-clusters of a given Leiden cluster for clarity and
2. isolate the Leiden clusters and visualize them in both UMAP space and physical (XY) space to see if there are regions in the tissue that might provide clues about the cell types.

Instead of the default plotDots colors, let’s define our own.

# define colors semi-manually instead of using the default colors
column <- 'leiden_pr'
column_levels <- levels(py$adata$obs[[column]])
n_levels <- length(column_levels)

if(n_levels<27){
  colors_use <- pals::alphabet(n_levels)
} else if(n < 53){
  colors_use <- c(pals::alphabet(26), pals::alphabet2(n_levels-26))
} else {
  stop("consider fewer groups")
}

names(colors_use) <- column_levels

# saving colors for later
results_list[['leiden_global_names']] <- names(colors_use)
results_list[['leiden_global_colors']] <- as.character(colors_use)
saveRDS(results_list, results_list_file)

Plot the cells in XY space and UMAP space and color based on leiden_pr.

group_prefix <- "leiden"

pp_assets_dir <- file.path(analysis_asset_dir, "preprocessing")

# XY (global only)
plotDots(py$adata, color_by='leiden_pr',
              plot_global = TRUE,
              facet_by_group = FALSE,
              additional_plot_parameters = list(
                  geom_point_params = list(
                    size=0.001
                  ),
                  scale_bar_params = list(
                    location = c(5, 0),
                    width = 2,
                    n = 3,
                    height = 0.1,
                    scale_colors = c("black", "grey30"),
                    label_nudge_y = -0.3
                  ),
                  directory = pp_assets_dir,
                  fileType = "png",
                  dpi = 200,
                  width = 8, 
                  height = 8,
                  prefix=group_prefix
                ),
              additional_ggplot_layers = list(
                theme_bw(),
                xlab("X (mm)"),
                ylab("Y (mm)"), 
                coord_fixed(),
                scale_color_manual(values = colors_use),
                theme(legend.position = c(0.8, 0.4)),
                guides(color = guide_legend(
                  title="Leiden (PR)",
                  override.aes = list(size = 3) ) )
              )
              )

# XY (facets only)
plotDots(py$adata, color_by='leiden_pr',
              plot_global = FALSE,
              facet_by_group = TRUE,
              additional_plot_parameters = list(
                  geom_point_params = list(
                    size=0.001
                  ),
                  scale_bar_params = list(
                    location = c(5, 0),
                    width = 2,
                    n = 3,
                    height = 0.1,
                    scale_colors = c("black", "grey30"),
                    label_nudge_y = -0.3
                  ),
                  directory = pp_assets_dir,
                  fileType = "png",
                  dpi = 100,
                  width = 5,
                  height = 5,
                  prefix=group_prefix
                ),
              additional_ggplot_layers = list(
                theme_bw(),
                xlab("X (mm)"),
                ylab("Y (mm)"), 
                coord_fixed(),
                scale_color_manual(values = colors_use),
                theme(legend.position = c(0.8, 0.4)),
                guides(color = guide_legend(
                  title="Leiden (PR)",
                  override.aes = list(size = 3) ) )
              )
              )

# UMAP (global only)
plotDots(py$adata, 
              obsm_key = "umap_pr",
              color_by='leiden_pr',
              plot_global = TRUE,
              facet_by_group = FALSE,
              additional_plot_parameters = list(
                  geom_point_params = list(
                    size=0.001, alpha=0.1
                  ),
                  geom_label_params = list(
                    size = 4
                  ),
                  labels_on_plot = data.frame(),
                  directory = pp_assets_dir,
                  fileType = "png",
                  dpi = 200,
                  width = 8,
                  height = 8,
                  prefix=group_prefix
                ),
              additional_ggplot_layers = list(
                theme_bw(),
                xlab("UMAP 1"),
                ylab("UMAP 2"), 
                coord_fixed(),
                scale_color_manual(values = colors_use),
                # guides(color = guide_legend(
                #   title="Cell Type",
                #   override.aes = list(size = 3) ) ), 
                theme(legend.position = "none")
              )
            )

# UMAP (facets only)
plotDots(py$adata, 
              obsm_key = "umap_pr",
              color_by='leiden_pr',
              plot_global = FALSE,
              facet_by_group = TRUE,
              additional_plot_parameters = list(
                  geom_point_params = list(
                    size=0.001, alpha=0.1
                  ),
                  geom_label_params = list(
                    size = 2
                  ),
                  labels_on_plot = data.frame(),
                  directory = pp_assets_dir,
                  fileType = "png",
                  dpi = 100,
                  width = 5,
                  height = 5,
                  prefix=group_prefix
                ),
              additional_ggplot_layers = list(
                theme_bw(),
                xlab("UMAP 1"),
                ylab("UMAP 2"), 
                coord_fixed(),
                scale_color_manual(values = colors_use),
                guides(color = guide_legend(
                  title="Cell Type",
                  override.aes = list(size = 3) ) )
              )
            )

1

in the plotting below, we will use this name to parse out files.

Here are the overall (global) plots.

Leiden - UMAP

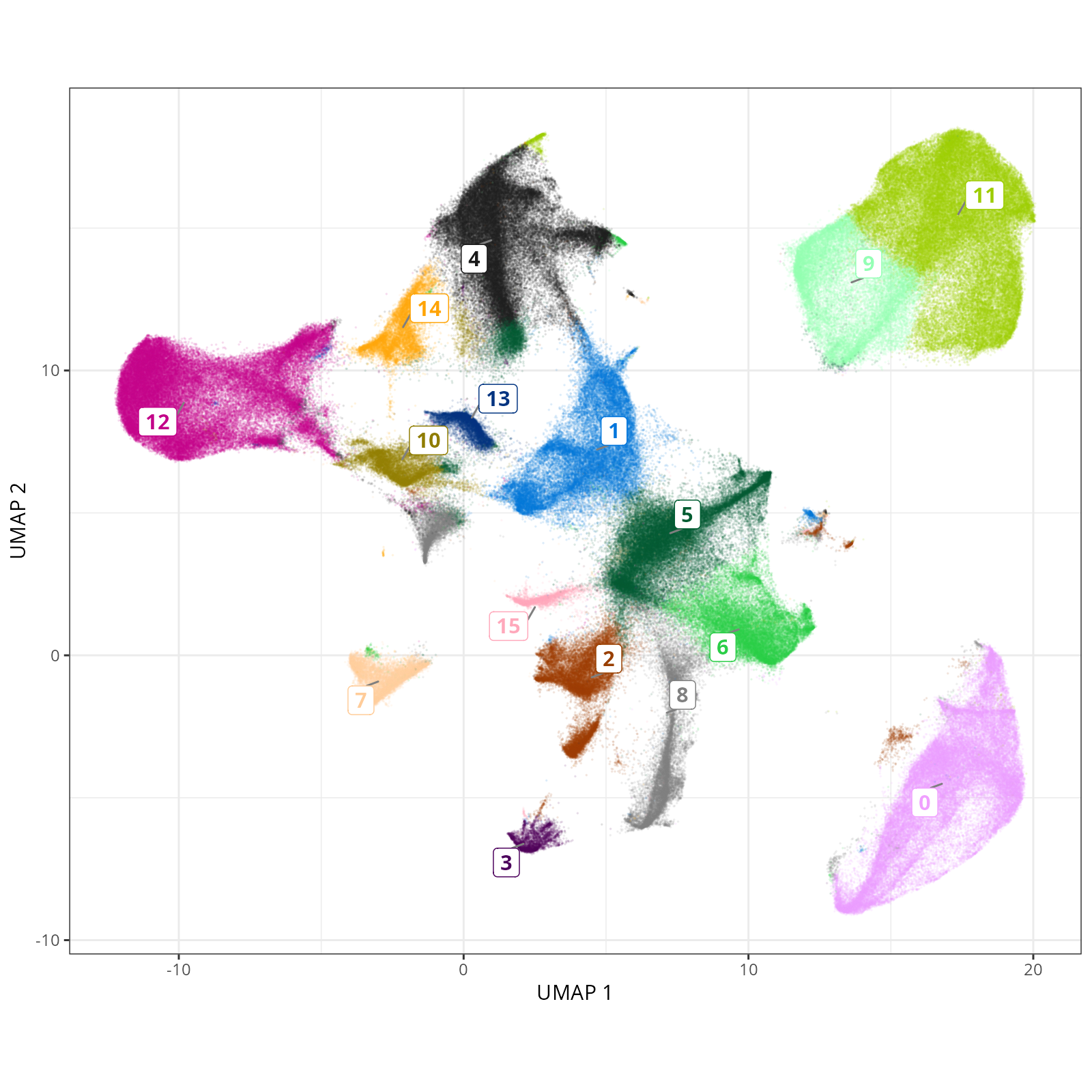
Figure 4.3: UMAP with Leiden (PR-based) cells.

Leiden - XY

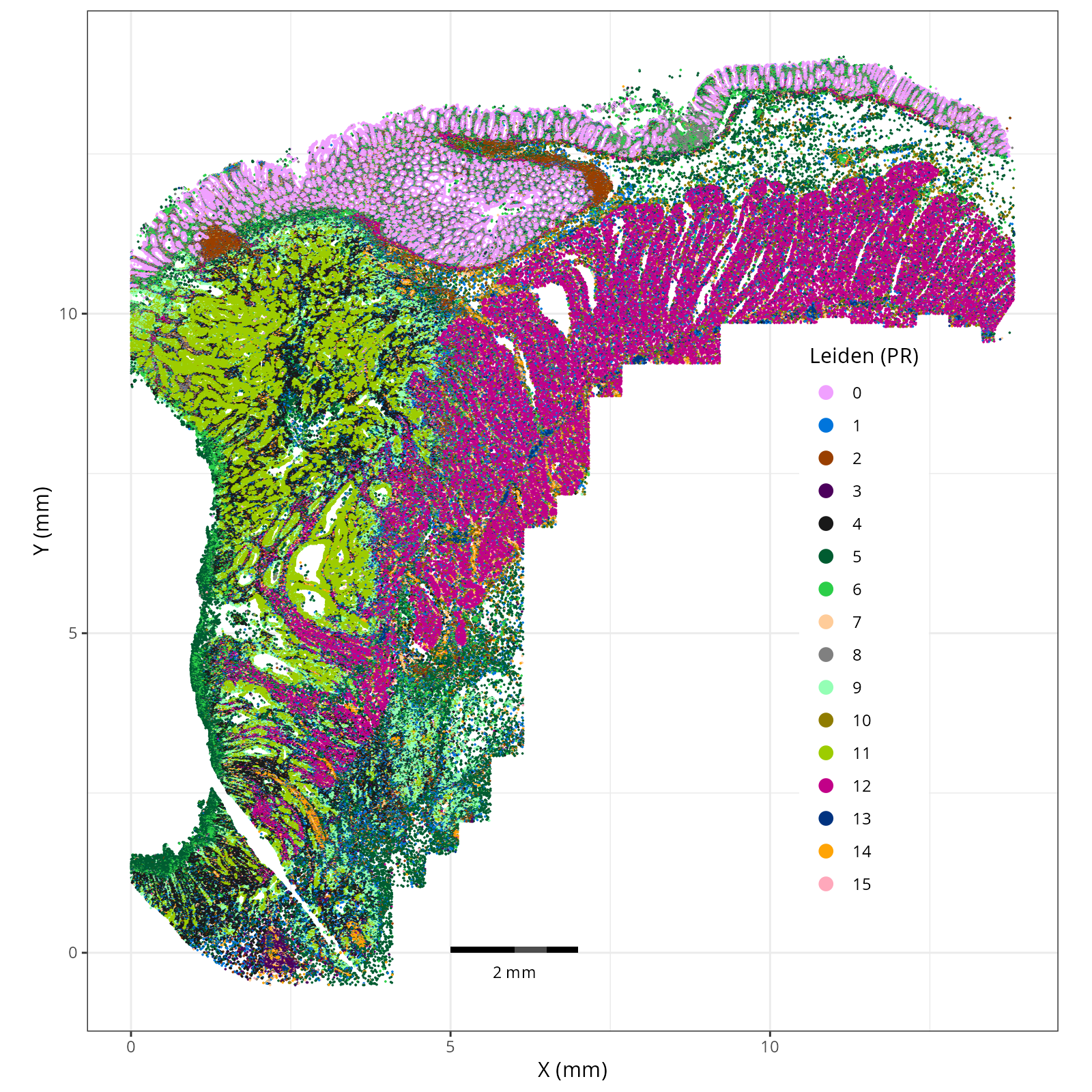
Figure 4.4: XY with Leiden (PR-based) cells.

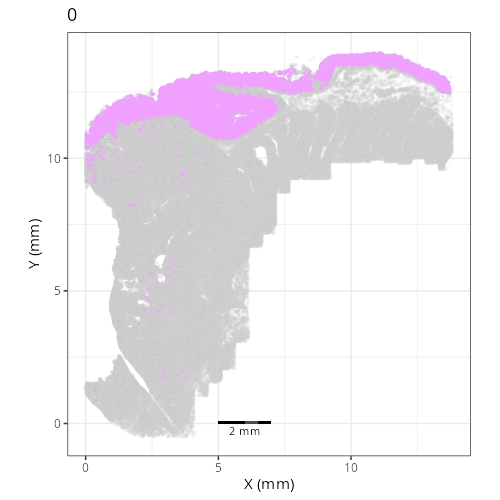
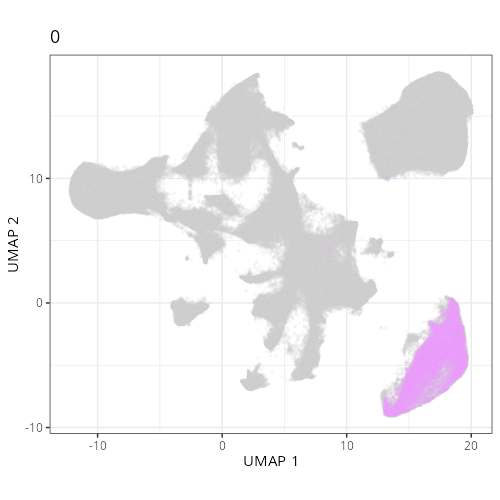
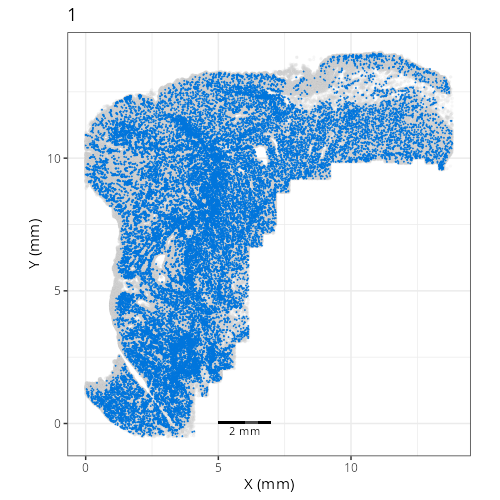
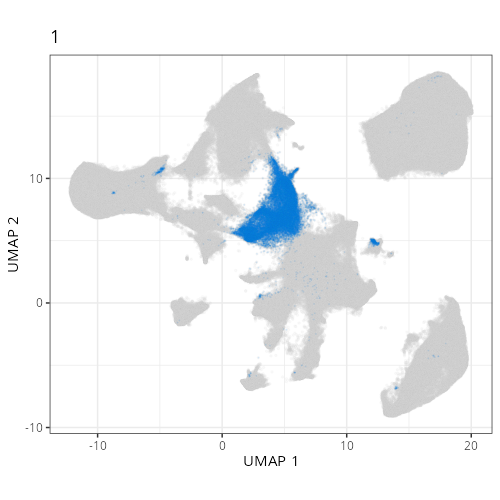
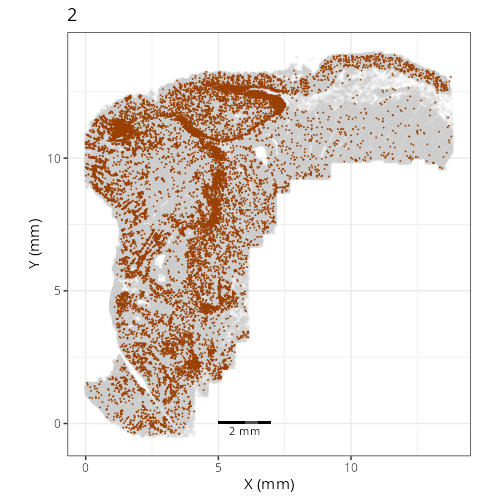
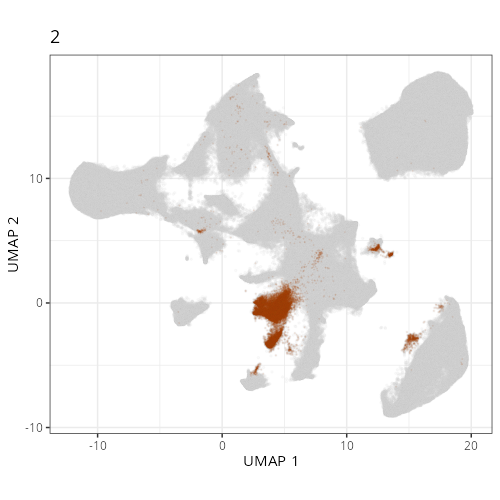
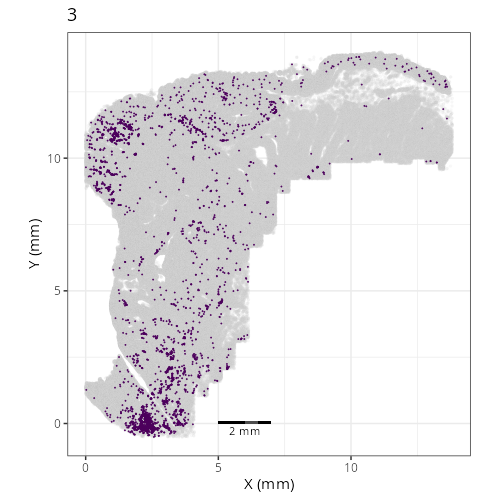
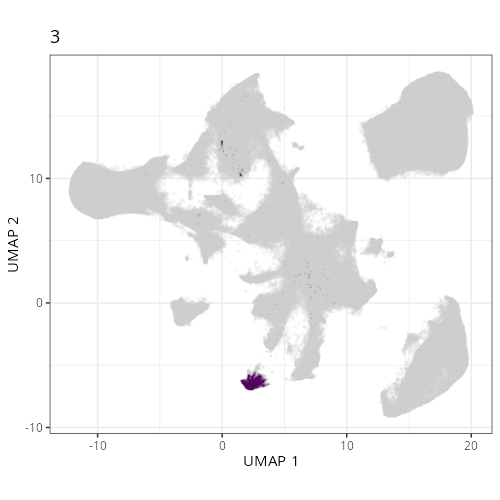
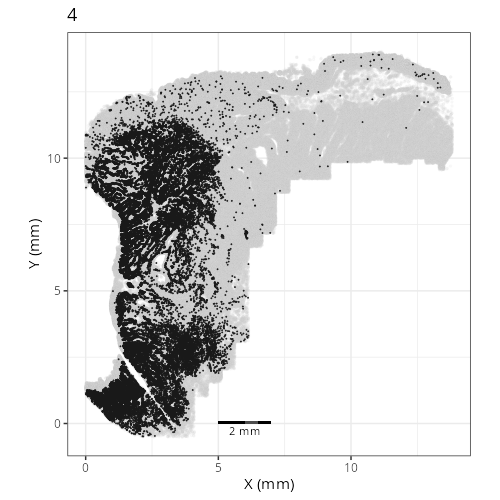
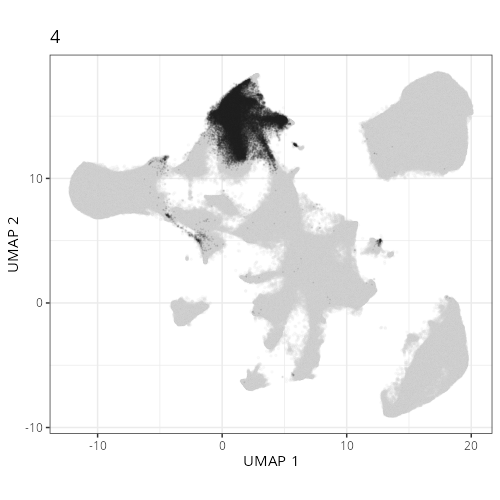
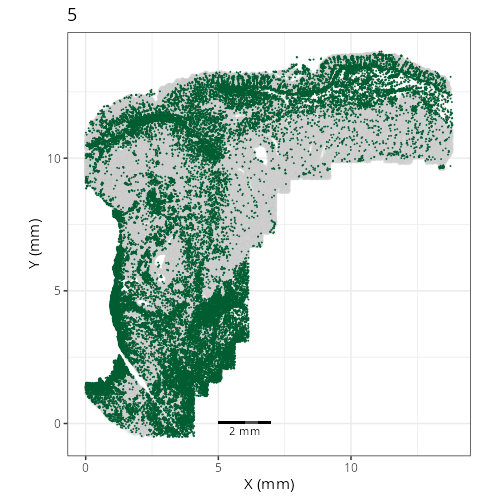
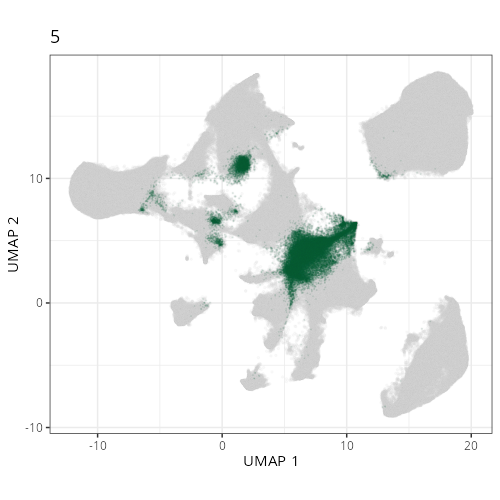
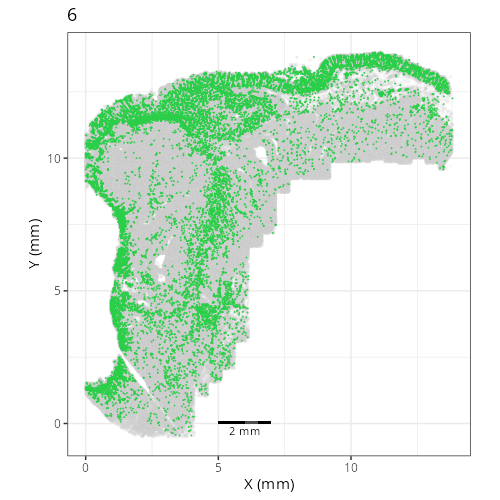
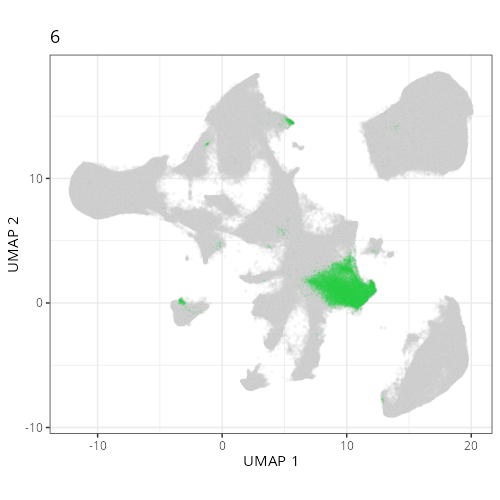
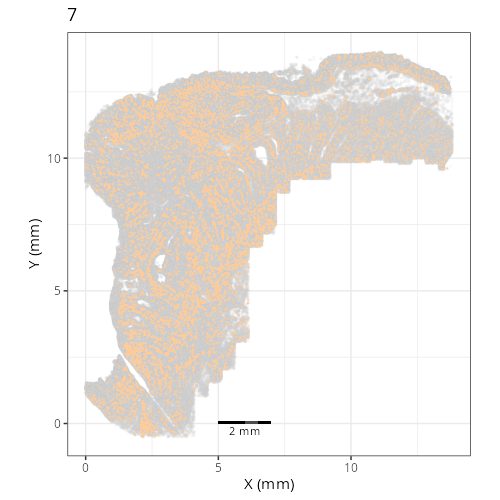
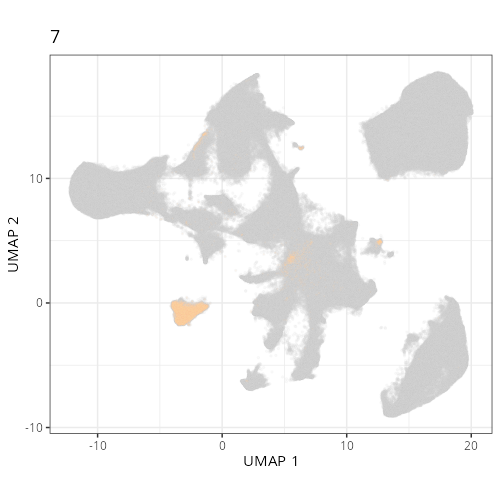
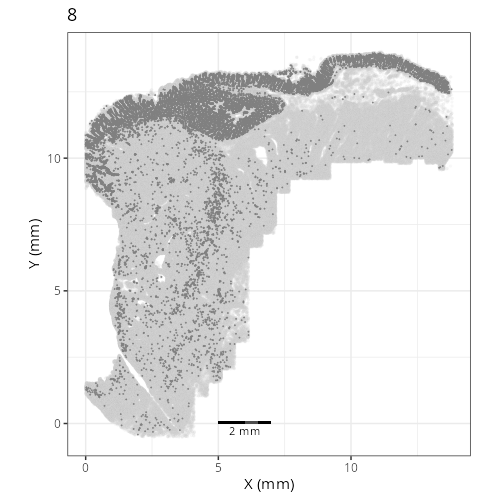
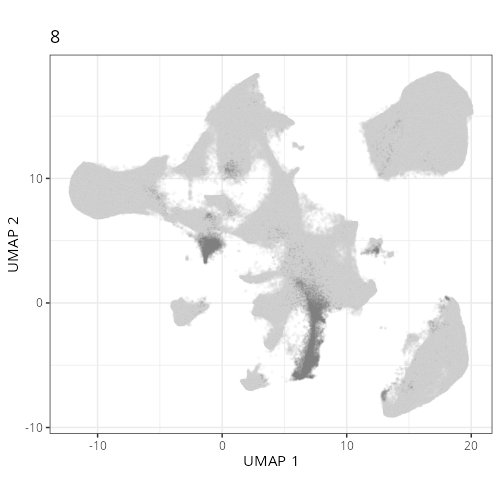
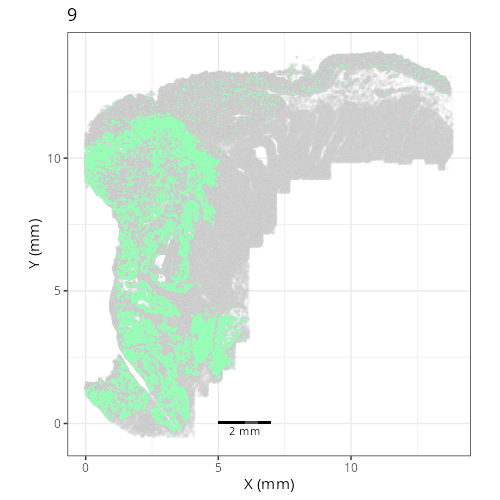
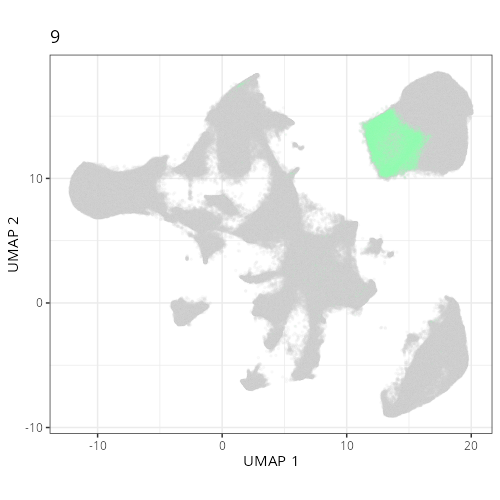
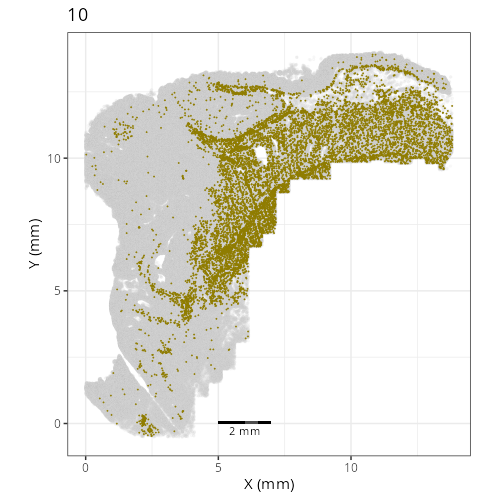
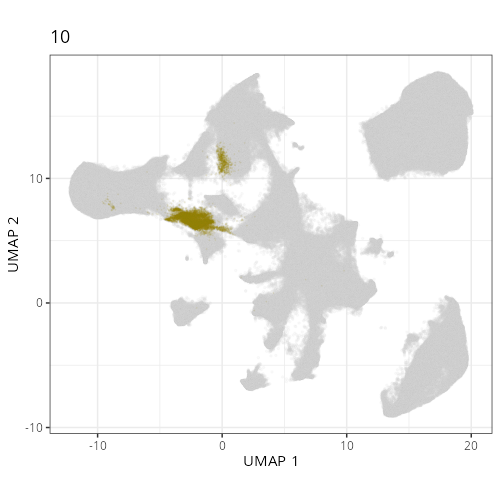
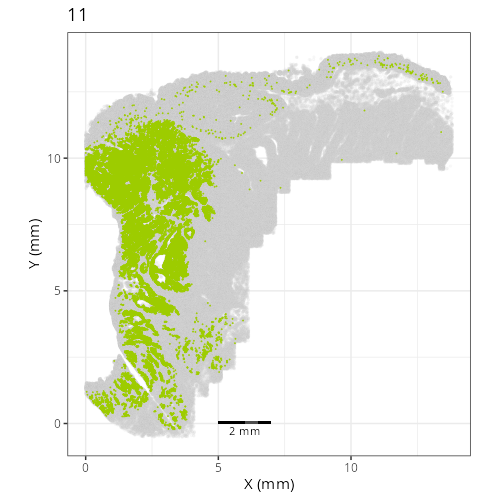
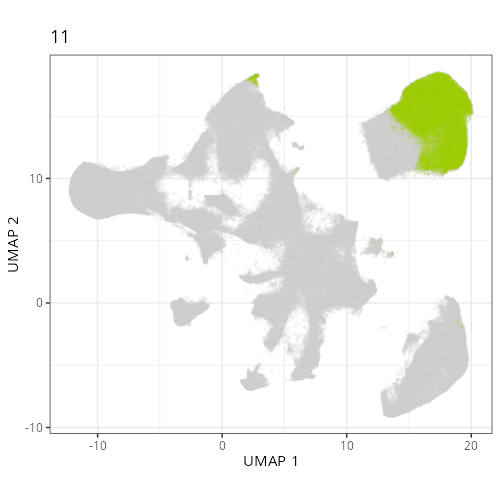
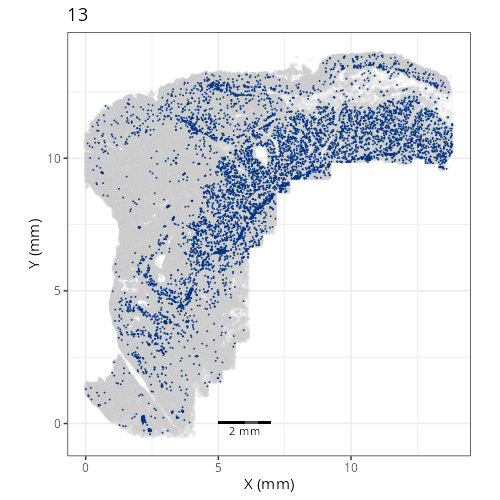
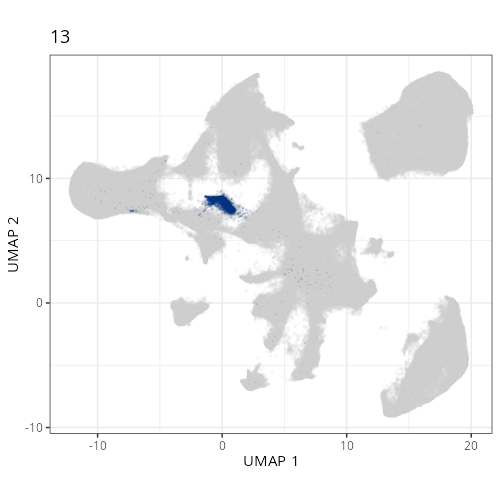
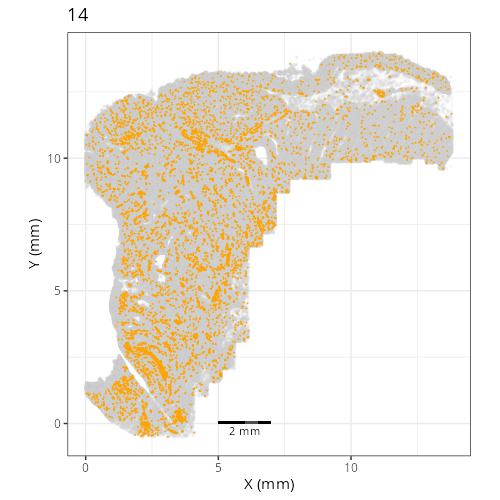
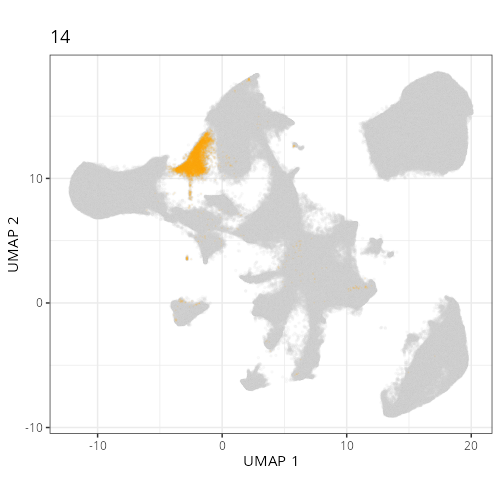
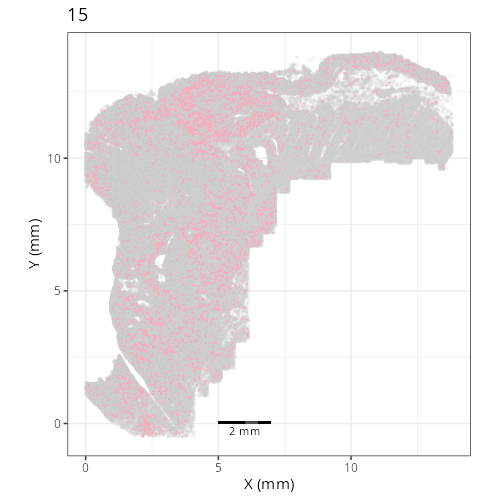
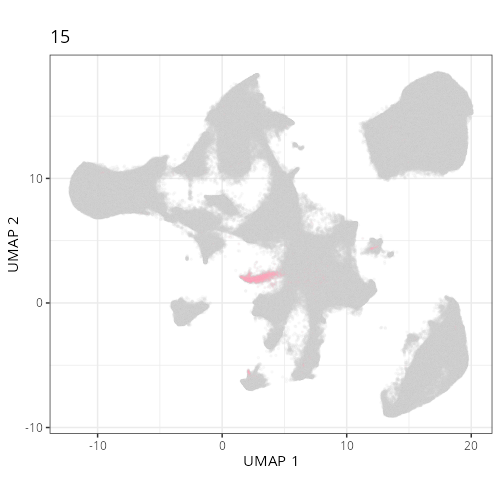
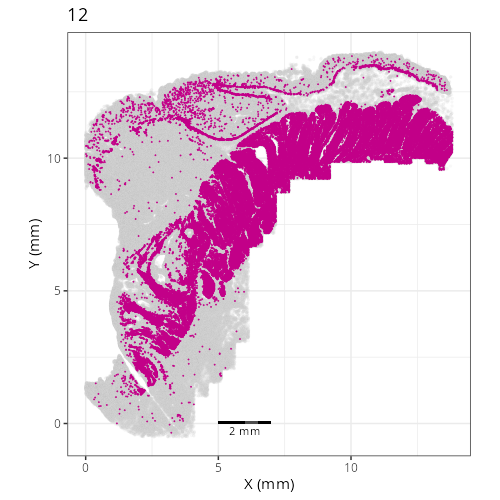
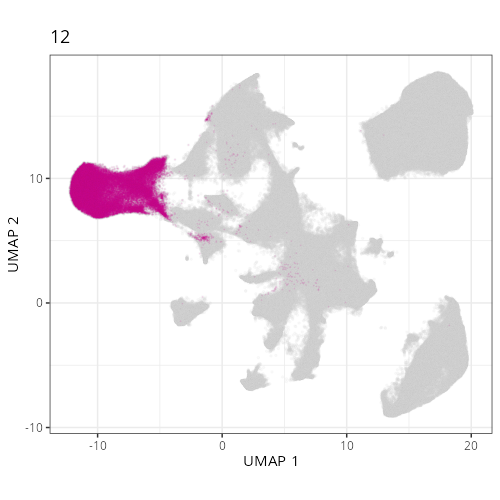
Here are the individual plots² we created organized by Leiden cluster. From these pairs of plots one can quickly see how some Leiden clusters are spatially restricted. For example, Leiden 0 consists of cells in the top part of the tissue (i.e., the non-tumoral epithelium). Similarly, cluster 12 occupies the left-most region of the tissue.

0

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

4.4 Conclusion

And with that, we’ve navigated the essential pre-processing steps. Starting with our quality-controlled cell data, we applied normalization to account for technical variations, identified the most informative genes, and used PCA to reduce the data’s dimensionality. Building upon this foundation, we generated UMAP embeddings for visualization and performed Leiden clustering to partition the cells into distinct groups based on their expression profiles.

The interactive exploration highlighted a critical point: parameters matter. Choices made during normalization, dimensionality reduction, and clustering significantly influence the final UMAP layout and cluster assignments. There isn’t a single “correct” set of parameters, but understanding their effects allows you to tailor the analysis to best reveal the biological structures relevant to your specific questions.

The resulting AnnData object, now enriched with normalized data layers, PCA coordinates, UMAP embeddings, and Leiden cluster labels, is primed for the next crucial phase: assigning biological meaning to these patterns. In the following chapters we will delve into grouping cells based on their spatial domain and their cell types.

1.

Hafemeister, C. & Satija, R. Normalization and variance stabilization of single-cell RNA-seq data using regularized negative binomial regression. Genome Biol. 20, 296 (2019).

---

1. when I tried using the sc.experimental.pp.normalize_pearson_residuals method on this dataset, the OS crashed (>200 GBs of RAM).

2. To see how to generate this type of output, click the </> icon on the top right of this chapter and then click view source.